Powder diffraction with spotty data … how to handle the spottiness.#
The data used for this tutorial are available on http://www.silx.org/pub/pyFAI/pyFAI_UM_2026/spotty/, it is a standard material SRM640, Silicon, recorded on the ID11 beamline with a sub-micron beam at 40 keV, using an Eiger2 CdTe detector at 200Hz. The Eiger file is the first data-file from a dataset containing 90 of them.
[1]:
%matplotlib inline
[2]:
import copy
import os
import glob
import time
import numpy
from matplotlib.pyplot import subplots
import fabio
from silx.resources import ExternalResources
import pyFAI
from pyFAI.gui import jupyter
start_time = time.perf_counter()
print(f"Using pyFAI version {pyFAI.version}")
Using pyFAI version 2026.1.0-dev0
[3]:
resource = ExternalResources("spotty", "http://www.silx.org/pub/pyFAI/pyFAI_UM_2026/spotty/")
Display the first and the average frame#
[4]:
fimg = fabio.open(resource.getfile("eiger_0000.h5"))
frame0 = fimg.data
fimg.nframes
[4]:
200
[5]:
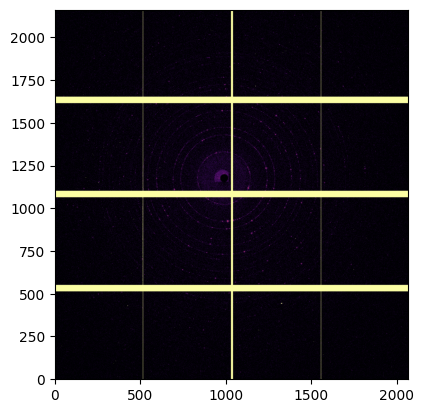
# display the image:
jupyter.display(frame0);
[6]:
%%time
# Average the dataset:
num = numpy.zeros(frame0.shape, dtype=numpy.int64) # Contains the sum of all signal
den = numpy.zeros(frame0.shape, dtype=numpy.int64) # Contains the number of contributing pixels
for frame in fimg:
num += numpy.where(frame.data<65535, frame.data, 0)
den += numpy.where(frame.data<65535, 1, 0)
avg = numpy.zeros(frame0.shape, dtype=numpy.float64)
numpy.divide(num, den, where=den!=0, out=avg);
CPU times: user 4.95 s, sys: 692 ms, total: 5.64 s
Wall time: 5.66 s
[7]:
jupyter.display(avg);
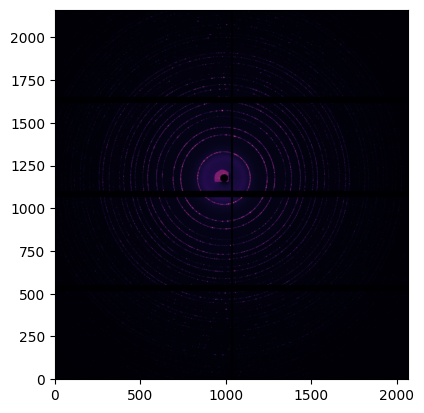
Perform the azimuthal integration and compare with sigma-clipping and median filtering#
First on needs to load the azimuthal integrator.
[8]:
ai = pyFAI.load(resource.getfile("ID11_40keV.poni"))
ai
[8]:
Detector Eiger2 CdTe 4M PixelSize= 75µm, 75µm BottomRight (3) CdTe,750µm
Wavelength= 0.305501 Å Parallax: off
SampleDetDist= 1.178702e-01 m PONI= 8.783056e-02, 7.342441e-02 m rot1=-0.005004 rot2=0.001866 rot3=0.000000 rad
DirectBeamDist= 117.872 mm Center: x=986.856, y=1174.007 pix Tilt= 0.306° tiltPlanRotation= 20.455° λ= 0.306Å
[9]:
# Common integration parameters:
kwargs = {"npt": 2000,
"unit": "2th_deg",
"method": ("no", "csr", "cython"),
"dummy": 65535,
}
[10]:
res_aver = ai.integrate1d(avg, **kwargs)
res_sigma = ai.sigma_clip_ng(avg, **kwargs, error_model="azimuthal")
res_median = ai.medfilt1d_ng(avg, **kwargs)
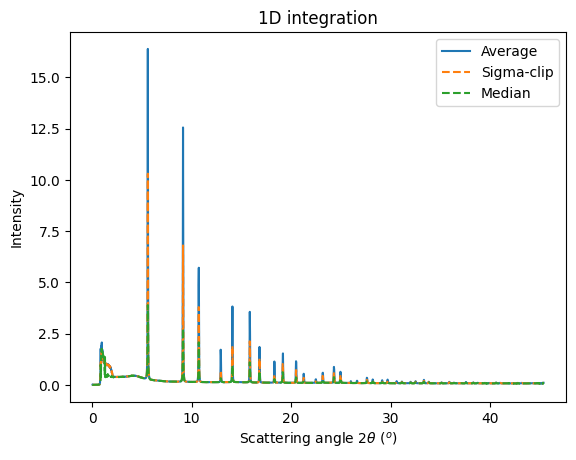
[11]:
ax = jupyter.plot1d(res_aver, label="Average")
ax.plot(*res_sigma[:2], "--" ,label="Sigma-clip")
ax.plot(*res_median[:2], "--" ,label="Median")
ax.legend();
Calculate the spottiness for the first and the average frame:#
[12]:
kwargs["error_model"] = "azimuthal"
res_avg = ai.integrate1d(avg, **kwargs)
res_fr0 = ai.integrate1d(frame0, **kwargs)
res_avg.calc_spottiness()
[12]:
0.025335838760482423
[13]:
print(f"Unweighted spottiness index: S(frame0)={res_fr0.calc_spottiness():.3f};\tS(avg)={res_avg.calc_spottiness():.3f}.")
print(f"I-Weighted spottiness index: S(frame0)={res_fr0.calc_spottiness(True):.3f};\tS(avg)={res_avg.calc_spottiness(True):.3f}.")
Unweighted spottiness index: S(frame0)=0.156; S(avg)=0.025.
I-Weighted spottiness index: S(frame0)=0.209; S(avg)=0.061.
Integrate all stack and plot spottiness for each frame in the stack#
[14]:
%%time
res = [ai.integrate1d(frame.data, **kwargs) for frame in fimg]
CPU times: user 2min 57s, sys: 206 ms, total: 2min 57s
Wall time: 8.01 s
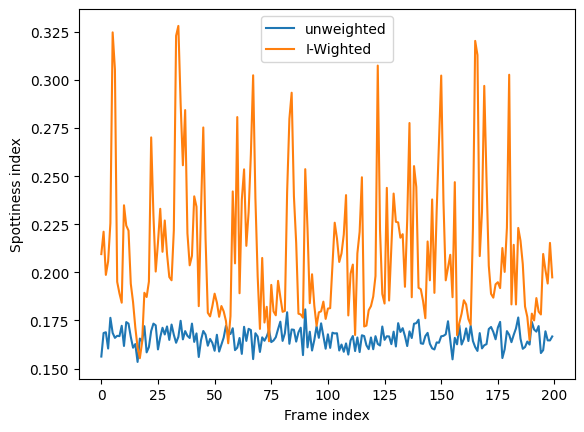
[15]:
fig,ax = subplots()
ax.plot([r.calc_spottiness() for r in res], label="unweighted")
ax.plot([r.calc_spottiness(weighted=True) for r in res], label="I-Wighted")
ax.set_xlabel("Frame index")
ax.set_ylabel("Spottiness index")
ax.legend();
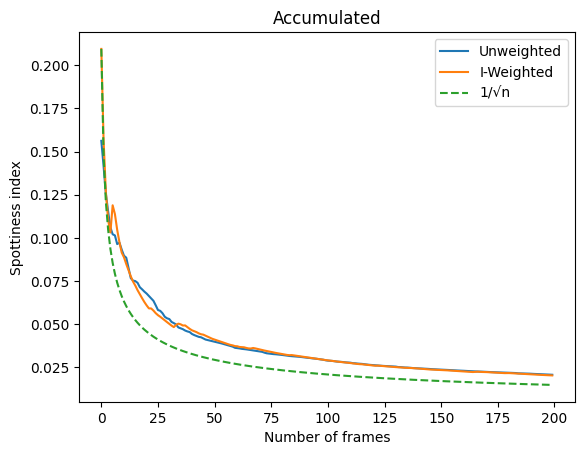
Accumulate frames to assess the evolution of spottiness with the number of frames#
This should evolve as \(1/\sqrt{N}\)
[16]:
# Accumulate 2 frames:
print("First", res[0].calc_spottiness())
print("Second", res[1].calc_spottiness())
print("1 + 2", res[1].union(res[0]).calc_spottiness())
First 0.15621348906463955
Second 0.16844202699901842
1 + 2 0.14151299563643194
[17]:
%%time
tmp = copy.deepcopy(res[0])
acc_u = [res[0].calc_spottiness()]
acc_w = [res[0].calc_spottiness(True)]
for i in res[1:]:
tmp = i.union(tmp)
acc_u.append(tmp.calc_spottiness())
acc_w.append(tmp.calc_spottiness(True))
CPU times: user 89.8 ms, sys: 0 ns, total: 89.8 ms
Wall time: 89.8 ms
[18]:
fig,ax = subplots()
ax.plot(acc_u, label="Unweighted")
ax.plot(acc_w, label="I-Weighted")
ax.plot(acc_w[0]/numpy.sqrt(1+numpy.arange(fimg.nframes)), "--", label="1/√n")
ax.set_ylabel("Spottiness index")
ax.set_xlabel("Number of frames")
ax.set_title("Accumulated")
ax.legend();
[19]:
fig,ax = subplots(2)
jupyter.plot1d(res_aver, label="Integrated averaged frame", ax=ax[0])
ax[0].plot(tmp.radial,tmp.intensity,"1", label="Accumulated results")
ax[0].set_title("Average before integration vs accumulate integrated results")
ax[0].legend()
ax[1].plot(tmp.radial,res_aver.intensity - tmp.intensity, label="delta")
ax[1].set_xlabel("Scattering angle")
ax[1].set_ylabel("Delta");
# ax[1].legend();
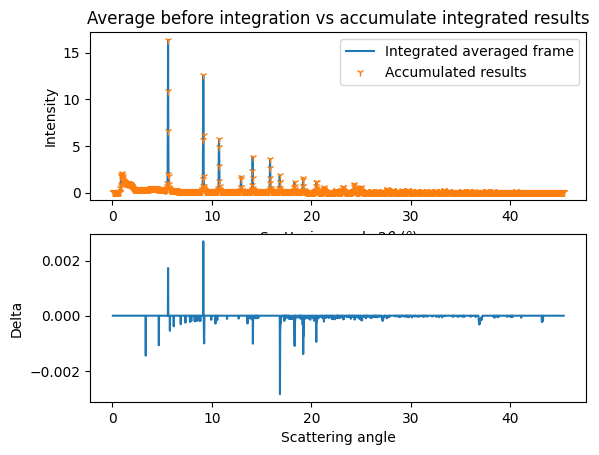
Conclusions:#
Merging data, especially when they come from a Dectris detector, requires careful handling of the dynamically masked pixels
Azimuthal integration and frame averaging can be interchanged, but only under certain conditions
It is possible to separate Bragg spots from powder signal using sigma-clipping or median filtering in azimuthal space
The spottiness of the integrated pattern can be measured if the “azimuthal” error model was used.
Residual spottiness evolves as \(1/\sqrt{N}\)
[20]:
print(f"Run-time: {time.perf_counter()-start_time:.3f}s")
Run-time: 20.163s
[ ]: