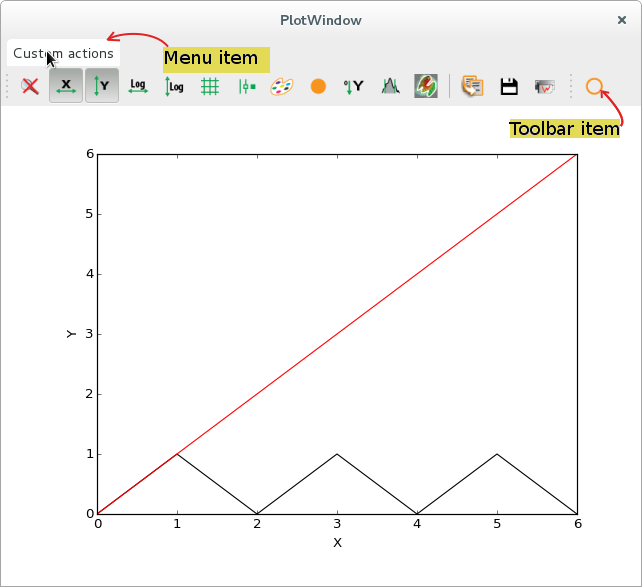
Adding custom plot actions#
PlotWindow defines a number of standard plot actions that can be executed
by clicking on toolbar icons.
Developers can design additional plot actions to be added as toolbar icons or as menu entries,
to be added to a PlotWindow or to design their own plot window based on
PlotWidget.
This documentation pages provide examples on how to do this.
Simple example: Shift a curve#
The following script is a simplistic example to show the required basic steps:
create a new class inheriting from
silx.gui.plot.actions.PlotActiondefine basic parameters such as the icon, the tooltip…
write a method that will be triggered by the plot action
initialise the new plot action by passing a reference to a plot window
add the plot action to a toolbar or a menu
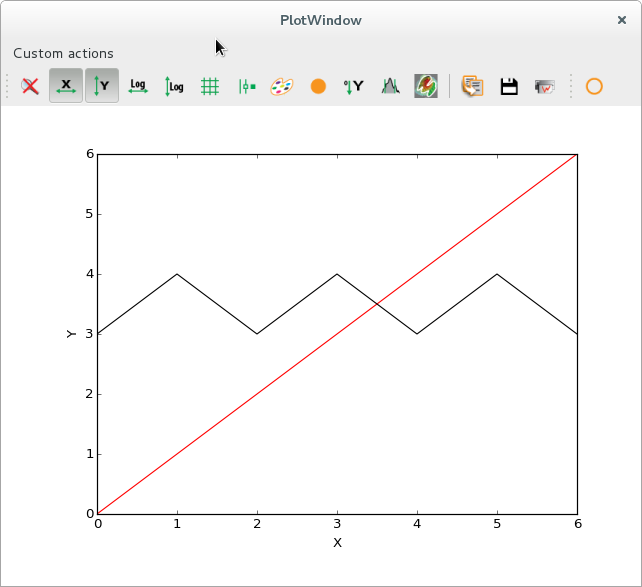
The method implemented in this action interacts with the plot in a basic way. It gets the active curve, then it creates a new data array based on the curve points, and finally it replaces the original curve by a new one using the modified data array.
import sys
from silx.gui import qt
from silx.gui.plot import PlotWindow
from silx.gui.plot.actions import PlotAction
class ShiftUpAction(PlotAction):
"""QAction shifting up a curve by one unit
:param plot: :class:`.PlotWidget` instance on which to operate
:param parent: See :class:`QAction`
"""
def __init__(self, plot, parent=None):
PlotAction.__init__(
self,
plot,
icon="shape-circle",
text="Shift up",
tooltip="Shift active curve up by one unit",
triggered=self.shiftActiveCurveUp,
parent=parent,
)
def shiftActiveCurveUp(self):
"""Get the active curve, add 1 to all y values, use this new y
array to replace the original curve"""
# By inheriting from PlotAction, we get access to attribute self.plot
# which is a reference to the PlotWindow
activeCurve = self.plot.getActiveCurve()
if activeCurve is None:
qt.QMessageBox.information(
self.plot, "Shift Curve", "Please select a curve."
)
else:
# Unpack curve data.
# Each curve is represented by an object with methods to access:
# the curve data, its legend, associated information and curve style
# Here we retrieve the x and y data of the curve
x0 = activeCurve.getXData()
y0 = activeCurve.getYData()
# Add 1 to all values in the y array
# and assign the result to a new array y1
y1 = y0 + 1.0
# Set the active curve data with the shifted y values
activeCurve.setData(x0, y1)
# creating QApplication is mandatory in order to use qt widget
app = qt.QApplication([])
sys.excepthook = qt.exceptionHandler
# create a PlotWindow
plotwin = PlotWindow()
# Add a new toolbar
toolbar = qt.QToolBar("My toolbar")
plotwin.addToolBar(toolbar)
# Get a reference to the PlotWindow's menu bar, add a menu
menubar = plotwin.menuBar()
actions_menu = menubar.addMenu("Custom actions")
# Initialize our action, give it plotwin as a parameter
myaction = ShiftUpAction(plotwin)
# Add action to the menubar and toolbar
toolbar.addAction(myaction)
actions_menu.addAction(myaction)
# Plot a couple of curves with synthetic data
x = [0, 1, 2, 3, 4, 5, 6]
y1 = [0, 1, 0, 1, 0, 1, 0]
y2 = [0, 1, 2, 3, 4, 5, 6]
plotwin.addCurve(x, y1, legend="triangle shaped curve")
plotwin.addCurve(x, y2, legend="oblique line")
plotwin.show()
app.exec()
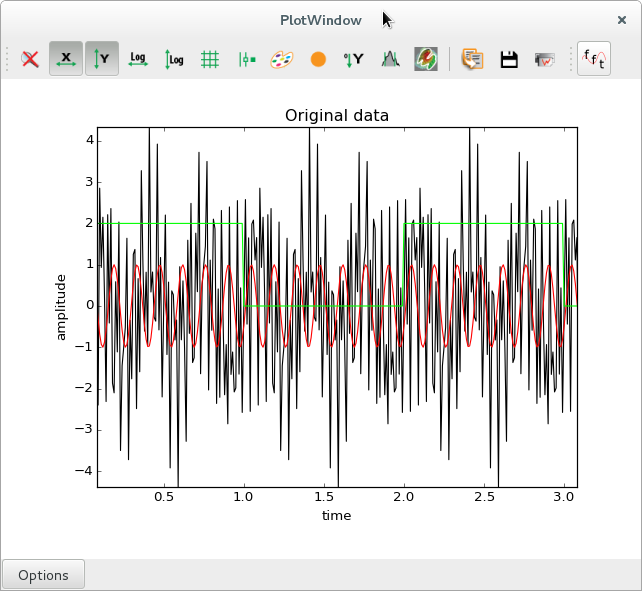
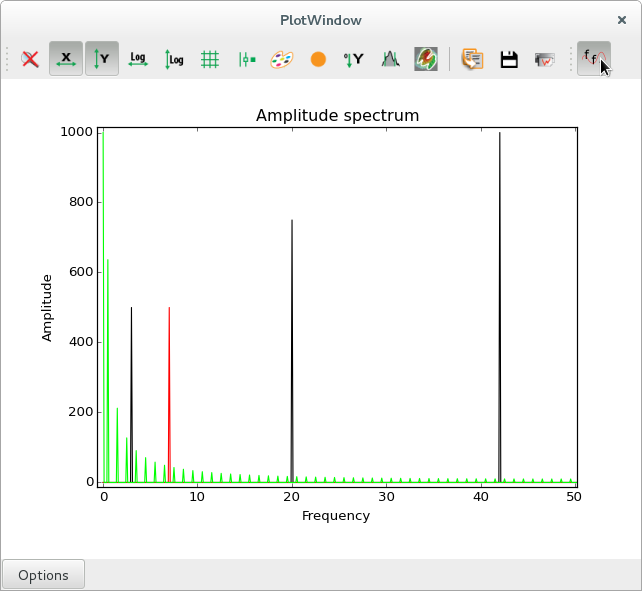
Advanced example: Display an amplitude spectrum#
This more advanced example (see figure below) shows additional ways of interacting with the plot, by changing labels, storing additional data arrays along with the curve coordinates.
This action is checkable, meaning that is has two states. When clicking the toolbar icon or the menu item, this remains in a pushed state until it is clicked again.
In one state (un-checked), the original data is displayed. In the other state, the amplitude spectrum of the original signal is displayed. When the state is changed, the triggered action computes either the Fast Fourier Transform (FFT), or the reverse FFT.
This example also illustrates how to store additional data along with a curve. The FFT computation returns complex values, but you want to display real data, so you compute the spectrum of amplitudes. However, the inverse FFT requires the complete FFT data as input. You are therefore required to store the complex array of FFT data as curve metadata, in order to be able to reverse the process when the action is unchecked.
import numpy
import os
import sys
from silx.gui import qt
from silx.gui.plot import PlotWindow
from silx.gui.plot.actions import PlotAction
# Custom icon
# make sure there is a "fft.png" file saved in the same folder as this script
scriptdir = os.path.dirname(os.path.realpath(__file__))
my_icon = os.path.join(scriptdir, "fft.png")
class FftAction(PlotAction):
"""QAction performing a Fourier transform on all curves when checked,
and reverse transform when unchecked.
:param plot: PlotWindow on which to operate
:param parent: See documentation of :class:`QAction`
"""
def __init__(self, plot, parent=None):
PlotAction.__init__(
self,
plot,
icon=qt.QIcon(my_icon),
text="FFT",
tooltip="Perform Fast Fourier Transform on all curves",
triggered=self.fftAllCurves,
checkable=True,
parent=parent,
)
def _rememberGraphLabels(self):
"""Store labels and title as attributes"""
self.original_title = self.plot.getGraphTitle()
self.original_xlabel = self.plot.getXAxis().getLabel()
self.original_ylabel = self.plot.getYAxis().getLabel()
def fftAllCurves(self, checked=False):
"""Get all curves from our PlotWindow, compute the amplitude spectrum
using a Fast Fourier Transform, replace all curves with their
amplitude spectra.
When un-checking the button, do the reverse transform.
:param checked: Boolean parameter signaling whether the action
has been checked or unchecked.
"""
allCurves = self.plot.getAllCurves(withhidden=True)
if checked:
# remember original labels
self._rememberGraphLabels()
# change them
self.plot.setGraphTitle("Amplitude spectrum")
self.plot.getXAxis().setLabel("Frequency")
self.plot.getYAxis().setLabel("Amplitude")
else:
# restore original labels
self.plot.setGraphTitle(self.original_title)
self.plot.getXAxis().setLabel(self.original_xlabel)
self.plot.getYAxis().setLabel(self.original_ylabel)
self.plot.clearCurves()
for curve in allCurves:
x = curve.getXData()
y = curve.getYData()
legend = curve.getName()
info = curve.getInfo()
if info is None:
info = {}
if checked:
# FAST FOURIER TRANSFORM
fft_y = numpy.fft.fft(y)
# amplitude spectrum
A = numpy.abs(fft_y)
# sampling frequency (samples per X unit)
Fs = len(x) / (max(x) - min(x))
# frequency array (abscissa of new curve)
F = [k * Fs / len(x) for k in range(len(A))]
# we need to store the complete transform (complex data) to be
# able to perform the reverse transform.
info["complex fft"] = fft_y
info["original x"] = x
# plot the amplitude spectrum
self.plot.addCurve(F, A, legend="FFT of " + legend, info=info)
else:
# INVERSE FFT
fft_y = info["complex fft"]
# we keep only the real part because we know the imaginary
# part is 0 (our original data was real numbers)
y1 = numpy.real(numpy.fft.ifft(fft_y))
# recover original info
x1 = info["original x"]
legend1 = legend[7:] # remove "FFT of "
# remove restored data from info dict
for key in ["complex fft", "original x"]:
del info[key]
# plot the original data
self.plot.addCurve(x1, y1, legend=legend1, info=info)
self.plot.resetZoom()
app = qt.QApplication([])
sys.excepthook = qt.exceptionHandler
plotwin = PlotWindow(control=True)
toolbar = qt.QToolBar("My toolbar")
plotwin.addToolBar(toolbar)
myaction = FftAction(plotwin)
toolbar.addAction(myaction)
# x range: 0 -- 10 (1000 points)
x = numpy.arange(1000) * 0.01
twopi = 2 * numpy.pi
# Sum of sine functions with frequencies 3, 20 and 42 Hz
y1 = (
numpy.sin(twopi * 3 * x)
+ 1.5 * numpy.sin(twopi * 20 * x)
+ 2 * numpy.sin(twopi * 42 * x)
)
# Cosine with frequency 7 Hz and phase pi / 3
y2 = numpy.cos(twopi * 7 * (x - numpy.pi / 3))
# 5 periods of square wave, amplitude 2
y3 = numpy.zeros_like(x)
for i in [0, 2, 4, 6, 8]:
y3[i * len(x) // 10 : (i + 1) * len(x) // 10] = 2
plotwin.addCurve(x, y1, legend="sin")
plotwin.addCurve(x, y2, legend="cos")
plotwin.addCurve(x, y3, legend="square wave")
plotwin.setGraphTitle("Original data")
plotwin.getYAxis().setLabel("amplitude")
plotwin.getXAxis().setLabel("time")
plotwin.show()
app.exec()
sys.excepthook = sys.__excepthook__
Original signals (zoomed in). In red, a cosine wave at 7 Hz. In black, a sum of sines with frequencies of 3, 20 and 42 Hz. In green, a square wave with a fundamental frequency of 0.5 Hz (period of 2 seconds). |
|
Amplitude spectra (zoomed in), with peaks visible at the expected frequencies of 3, 7, 20 and 42 Hz for the sine and cosine signals, respectively. In green, one sees the complete series of peaks related to the square wave, with a fundamental frequency at 0.5 Hz and harmonic frequencies at every odd multiple of the fundamental frequency. |