Inpainting missing data
Missing data in an image can be an issue, especially when one wants to perform Fourier analysis. This tutorial explains how to fill-up missing pixels with values which looks “realistic” and introduce as little perturbation as possible for subsequent analysis. The user should keep the mask nearby and only consider the values of actual pixels and never the one inpainted.
This tutorial will use fully synthetic data to allow comparison between actual (syntetic) data with inpainted values.
The first part of the tutorial is about the generation of a challenging 2D diffraction image with realistic noise and to describe the metric used, then comes the actual tutorial on how to use the inpainting. Finally a benchmark is used based on the metric determined.
Creation of the image
A realistic challenging image should contain:
Bragg peak rings. We chose LaB6 as guinea-pig, with very sharp peaks, at the limit of the resolution of the detector
Some amorphous content
strong polarization effect
Poissonian noise
One image will be generated but then multiple ones with different noise to discriminate the effect of the noise from other effects.
[1]:
%matplotlib inline
# Used for documentation to inline plots into notebook
# %matplotlib widget
# uncomment the later for better UI
from matplotlib.pyplot import subplots
import numpy
[2]:
import pyFAI
print("Using pyFAI version: ", pyFAI.version)
from pyFAI.azimuthalIntegrator import AzimuthalIntegrator
from pyFAI.gui import jupyter
import pyFAI.test.utilstest
from pyFAI.calibrant import get_calibrant
import time
start_time = time.perf_counter()
Using pyFAI version: 2023.10.0-dev0
[3]:
detector = pyFAI.detector_factory("Pilatus2MCdTe")
mask = detector.mask.copy()
nomask = numpy.zeros_like(mask)
detector.mask=nomask
ai = AzimuthalIntegrator(detector=detector)
ai.setFit2D(200, 200, 200)
ai.wavelength = 3e-11
print(ai)
Detector Pilatus CdTe 2M PixelSize= 1.720e-04, 1.720e-04 m
Wavelength= 3.000000e-11 m
SampleDetDist= 2.000000e-01 m PONI= 3.440000e-02, 3.440000e-02 m rot1=0.000000 rot2=0.000000 rot3=0.000000 rad
DirectBeamDist= 200.000 mm Center: x=200.000, y=200.000 pix Tilt= 0.000° tiltPlanRotation= 0.000° 𝛌= 0.300Å
[4]:
LaB6 = get_calibrant("LaB6")
LaB6.wavelength = ai.wavelength
print(LaB6)
r = ai.array_from_unit(unit="q_nm^-1")
decay_b = numpy.exp(-(r-50)**2/2000)
bragg = LaB6.fake_calibration_image(ai, Imax=1e4, W=1e-6) * ai.polarization(factor=1.0) * decay_b
decay_a = numpy.exp(-r/100)
amorphous = 1000*ai.polarization(factor=1.0)*ai.solidAngleArray() * decay_a
img_nomask = bragg + amorphous
#Not the same noise function for all images two images
img_nomask = numpy.random.poisson(img_nomask)
img_nomask2 = numpy.random.poisson(img_nomask)
img = numpy.random.poisson(img_nomask)
img[numpy.where(mask)] = -1
fig,ax = subplots(1,2, figsize=(10,5))
jupyter.display(img=img, label="With mask", ax=ax[0])
jupyter.display(img=img_nomask, label="Without mask", ax=ax[1])
LaB6 Calibrant with 640 reflections at wavelength 3e-11
[4]:
<Axes: title={'center': 'Without mask'}>
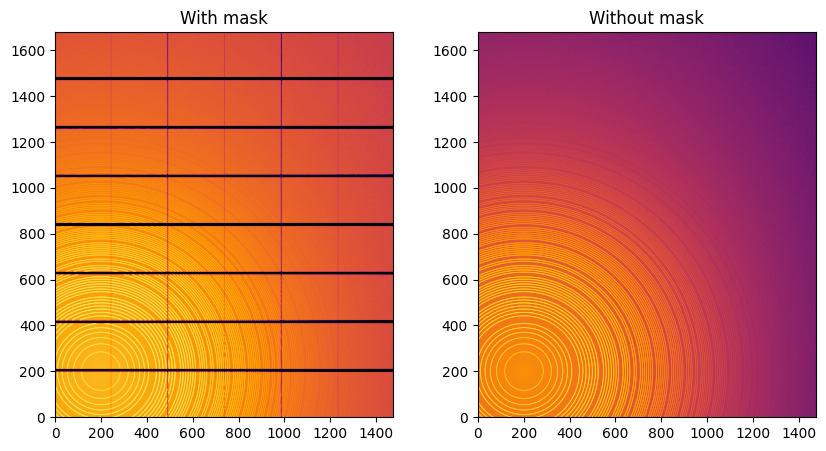
Note the aliassing effect on the displayed images.
We will measure now the effect after 1D intergeration. We do not correct for polarization on purpose to highlight the defect one wishes to whipe out. We use a R-factor to describe the quality of the 1D-integrated signal.
[5]:
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wo2 = ai.integrate1d(img_nomask2, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wm = ai.integrate1d(img, 2000, unit="q_nm^-1", method="splitpixel", mask=mask, radial_range=(0,210))
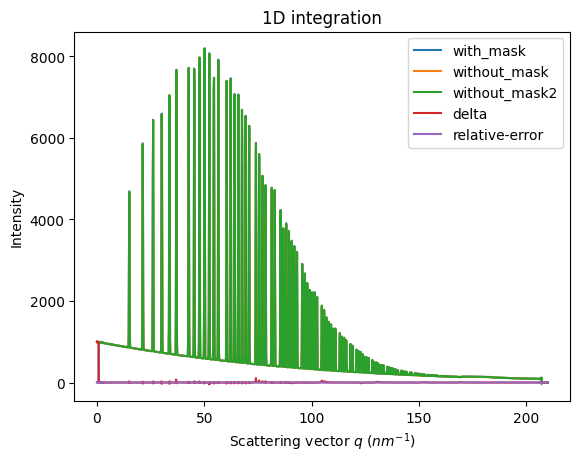
ax = jupyter.plot1d(wm , label="with_mask")
ax.plot(*wo, label="without_mask")
ax.plot(*wo2, label="without_mask2")
ax.plot(wo.radial, wo.intensity-wm.intensity, label="delta")
ax.plot(wo.radial, wo.intensity-wo2.intensity, label="relative-error")
ax.legend()
print("Between masked and non masked image R= %s"%pyFAI.utils.mathutil.rwp(wm,wo))
print("Between two different non-masked images R'= %s"%pyFAI.utils.mathutil.rwp(wo2,wo))
Between masked and non masked image R= 5.672788607265195
Between two different non-masked images R'= 0.450718545240364
[6]:
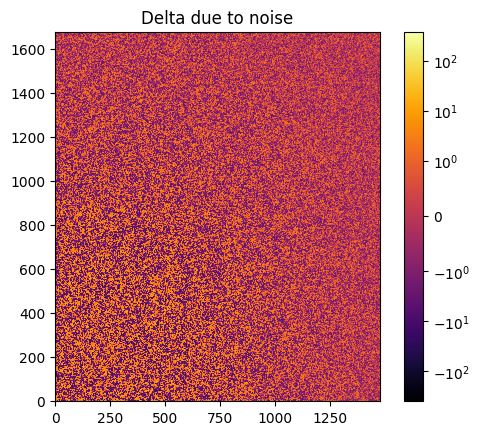
# Effect of the noise on the delta image
fig, ax = subplots()
jupyter.display(img=img_nomask-img_nomask2, label="Delta due to noise", ax=ax)
ax.figure.colorbar(ax.images[0])
[6]:
<matplotlib.colorbar.Colorbar at 0x7f6e3956b450>
Inpainting
This part describes how to paint the missing pixels for having a “natural-looking image”. The delta image contains the difference with the original image
[7]:
#Inpainting:
inpainted = ai.inpainting(img, mask=mask, poissonian=True)
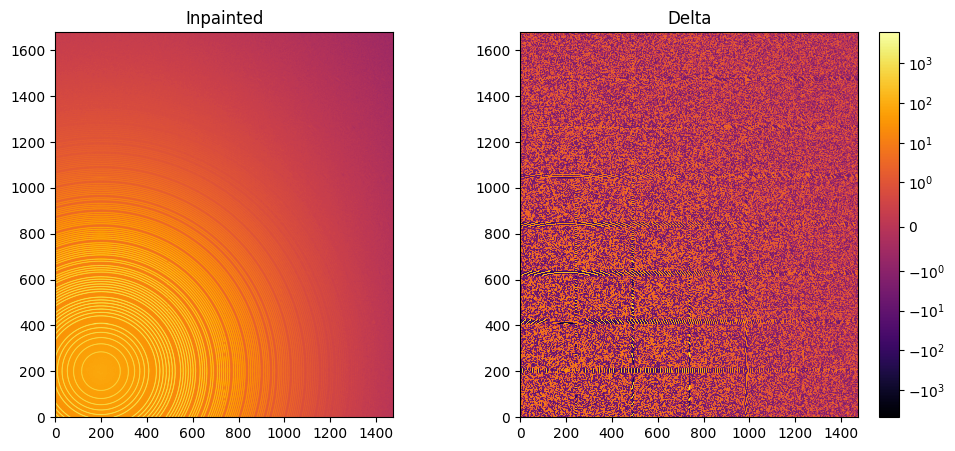
fig, ax = subplots(1, 2, figsize=(12,5))
jupyter.display(img=inpainted, label="Inpainted", ax=ax[0])
jupyter.display(img=img_nomask-inpainted, label="Delta", ax=ax[1])
ax[1].figure.colorbar(ax[1].images[0])
[7]:
<matplotlib.colorbar.Colorbar at 0x7f6e39554b50>
[8]:
# Comparison of the inpained image with the original one:
wm = ai.integrate1d(inpainted, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
ax = jupyter.plot1d(wm , label="inpainted")
ax.plot(*wo, label="without_mask")
ax.plot(wo.radial, wo.intensity-wm.intensity, label="delta")
ax.legend()
print("R= %s"%pyFAI.utils.mathutil.rwp(wm,wo))
R= 1.2551261451881464
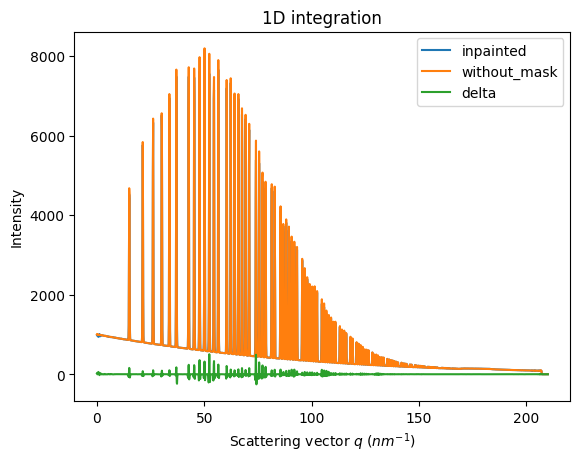
One can see by zooming in that the main effect on inpainting is a broadening of the signal in the inpainted region. This could (partially) be adressed by increasing the number of radial bins used in the inpainting.
Benchmarking and optimization of the parameters
The parameter set depends on the detector, the experiment geometry and the type of signal on the detector. Finer detail require finer slicing.
[9]:
#Basic benchmarking of execution time for default options:
%timeit inpainted = ai.inpainting(img, mask=mask)
3.25 s ± 392 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
[10]:
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
for m in (("no", "histogram", "cython"), ("bbox", "histogram","cython")):
for k in (512, 1024, 2048, 4096):
ai.reset()
for i in (0, 1, 2, 4, 8):
inpainted = ai.inpainting(img, mask=mask, poissonian=True, method=m, npt_rad=k, grow_mask=i)
wm = ai.integrate1d(inpainted, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
print(f"method: {m} npt_rad={k} grow={i}; R= {pyFAI.utils.mathutil.rwp(wm,wo)}")
method: ('no', 'histogram', 'cython') npt_rad=512 grow=0; R= 7.841700884084947
method: ('no', 'histogram', 'cython') npt_rad=512 grow=1; R= 7.840567861675538
method: ('no', 'histogram', 'cython') npt_rad=512 grow=2; R= 7.841912138663817
method: ('no', 'histogram', 'cython') npt_rad=512 grow=4; R= 7.840571673600346
method: ('no', 'histogram', 'cython') npt_rad=512 grow=8; R= 7.84152483658409
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=0; R= 8.088676314545005
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=1; R= 8.088577296800672
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=2; R= 8.088852666794153
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=4; R= 8.088612338121164
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=8; R= 8.088648687039049
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=0; R= 8.208372097414383
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=1; R= 8.20815605713825
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=2; R= 8.208313366587294
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=4; R= 8.208587651393247
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=8; R= 8.208334670209519
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=0; R= 8.283276354548496
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=1; R= 8.28337571144994
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=2; R= 8.283146997834441
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=4; R= 8.283354134827308
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=8; R= 8.28320750042507
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=0; R= 3.161098499255603
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=1; R= 2.897230421534965
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=2; R= 2.700367271544123
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=4; R= 2.6173090722944607
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=8; R= 2.5361086360786484
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=0; R= 1.6760549083226348
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=1; R= 1.3175822423843901
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=2; R= 1.309432250417557
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=4; R= 1.2726162580677667
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=8; R= 1.2671837650688433
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=0; R= 0.885924746298683
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=1; R= 0.6444818432899799
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=2; R= 0.628226813891081
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=4; R= 0.6281269950976757
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=8; R= 0.6241901411871493
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=0; R= 0.5518110675492013
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=1; R= 0.3954172035636847
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=2; R= 0.40523388475374905
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=4; R= 0.40095982885140063
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=8; R= 0.39820479091061034
[11]:
#Inpainting, best solution found:
ai.reset()
%time inpainted = ai.inpainting(img, mask=mask, poissonian=True, method=("pseudo", "csr", "cython"), npt_rad=4096, grow_mask=1)
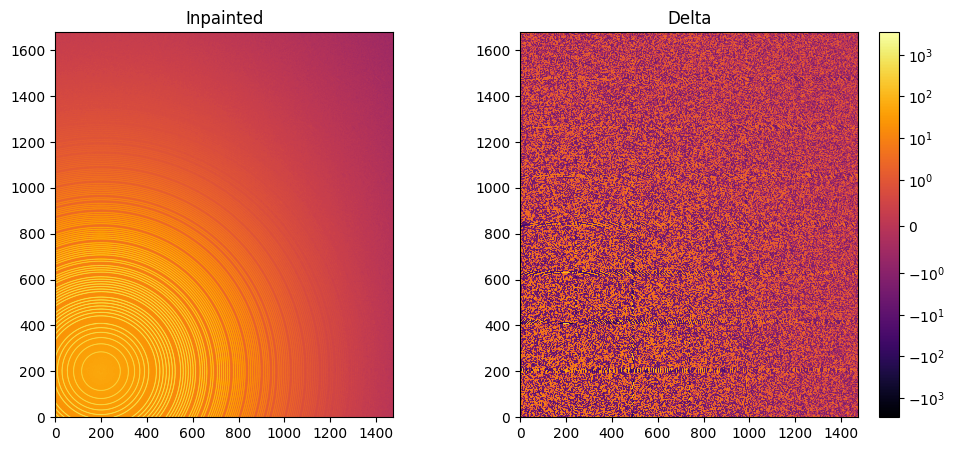
fig, ax = subplots(1, 2, figsize=(12, 5))
jupyter.display(img=inpainted, label="Inpainted", ax=ax[0])
jupyter.display(img=img_nomask-inpainted, label="Delta", ax=ax[1])
ax[1].figure.colorbar(ax[1].images[0])
pass
CPU times: user 4.48 s, sys: 143 ms, total: 4.63 s
Wall time: 4.34 s
[12]:
# Comparison of the inpained image with the original one:
wm = ai.integrate1d(inpainted, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
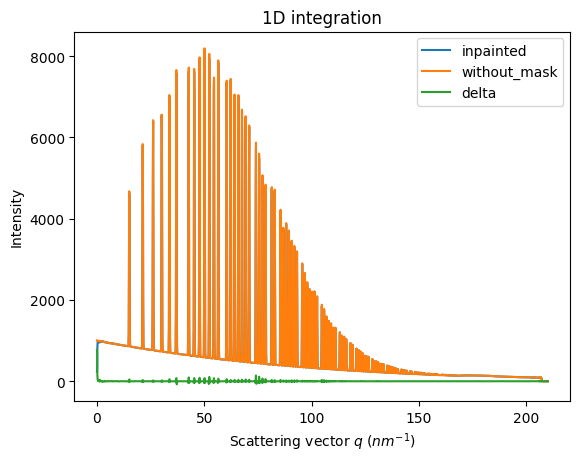
ax = jupyter.plot1d(wm , label="inpainted")
ax.plot(*wo, label="without_mask")
ax.plot(wo.radial, wo.intensity-wm.intensity, label="delta")
ax.legend()
print("R= %s"%pyFAI.utils.mathutil.rwp(wm,wo))
R= 1.6714881617547213
Conclusion
Inpainting is one of the only solution to fill up the gaps in detector when Fourier analysis is needed. This tutorial explains basically how this is possible using the pyFAI library and how to optimize the parameter set for inpainting. The result may greatly vary with detector position and tilt and the kind of signal (amorphous or more spotty).
[13]:
print(f"Execution time: {time.perf_counter()-start_time:.3f} s")
Execution time: 109.050 s